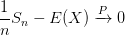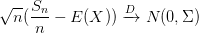1. Why Sampling
A misconception I used to have is that the era of big data means the end of a need for sampling, actually, in a Big Data project, like the Bosch production line performance prediction, our models are still developed and piloted with samples. More generally speaking, to understand a statistical task, most times we have to design experiments which will inevitably use sampling.
A sample is drawn with the goal of measuring something(with a sample statistic), or modeling something with a statistical/machine learning model. Much of classical statistics is concerned with making inference from small samples to populations: we do that by constructing Statistic, i.e. function of sample data to measure different features of population. Naturally we need to analyze sampling distribution, it refers to the distribution of some Sample Statistic.
2. Supporting Theorem
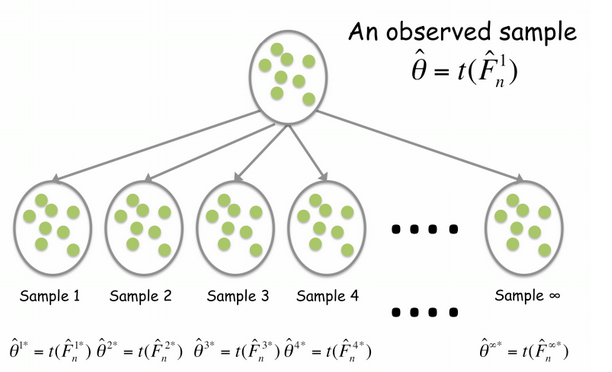
3. Magic – The Bootstrap
Key Idea: Treat the sample as if it were the population
Think about this: you got 2 samples s1 & s2 with the same size, they have the same point estimate of population mean, but std(s1)>>std(s2), how would you judge the accuracy of the point estimation? Obviously, you will trust s2 more. That is why bootstrap sampling works, it’s actually extracting as much information as possible from the sample.